3 métodos simples para aprender a multiplicar sem calculadora

Fazer conta é, para muitos, um pesadelo. E a calculadora acaba se tornando uma grande aliada.

Mas, no caso da multiplicação, há formas alternativas - e mais visuais - de se resolver as operações.

• Como Isaac Newton perdeu milhões com ações
• Por que as pessoas gastam demais nas férias?
• Por que os juros bancários para o consumidor caem menos que a Selic?

É provável que você tenha aprendido o método tradicional de multiplicação na escola. Ou seja: primeiro você decora a tabuada para, em seguida, multiplicar número a número.

E, se os números a serem multiplicados têm vários dígitos, você acaba precisando de um pedaço de papel para fazer a conta, como ilustra a imagem abaixo.

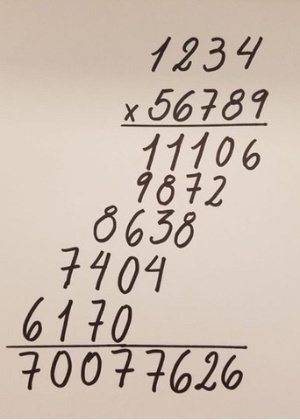
Existem, no entanto, outros métodos menos conhecidos que ajudam a entender a lógica da multiplicação.

E alguns são bastante visuais - envolvem traços, linhas e pontos. A BBC lista três, que acompanham vídeos que tornam a compreensão mais fácil, para você:

1. Método maia, também conhecido como japonês

Há várias teorias sobre a origem desse método.

Alguns dizem que foi inventado pela civilização maia, que habitou a América Central até a chegada dos colonizadores espanhóis no século 15.

Mas é também chamado de método japonês, uma vez que é usado pelos professores do país para ensinar multiplicação nas escolas.

Trata-se de um sistema de multiplicação com linhas. Ele consiste em desenhar linhas paralelas e perpendiculares para representar os dígitos dos números a serem multiplicados.

Por exemplo: 23 x 41.

Desenhamos duas linhas paralelas para representar o 2, e outras três linhas paralelas para representar o 3.

Na sequência, desenhamos, de forma perpendicular, quatro linhas paralelas para o 4 e uma linha para o 1.

Uma vez que a imagem está pronta, somam-se os pontos que se formam nas interseções.

E assim, chegamos ao resultado: 943, o mesmo obtido pela forma tradicional de multiplicação.

Achou muito difícil?

2. Método de multiplicação hindu

A origem desse método também não é muito clara, mas certamente passa pela Ásia.

"Esse método foi levado da Índia para a China e a Arábia, de onde foi para a Itália, entre os séculos 14 e 15, e recebeu o nome de gelosia, devido à semelhança com as persianas venezianas", explica o pesquisador Mario Roberto Canales Villanueva, em seu estudo exploratório sobre o uso de modelos alternativos para ensino e aprendizagem da multiplicação em Honduras.

Esse método prevê desenhar uma tabela - a quantidade de colunas e linhas vai variar de acordo com o número de algarismos na operação.

Vamos usar o mesmo exemplo anterior: 23 x 41.

Neste caso, são necessárias duas colunas e duas linhas - para as quais atribuímos os respectivos algarismos em sentido horário. Na sequência, dividimos cada campo da tabela com uma linha diagonal.

Os triângulos formados, a partir da divisão, devem ser preenchidos com o resultado da multiplicação do algarismo de cada coluna com o da linha correspondente. Para isso, precisamos decompor o resultado - a dezena é inserida no primeiro triângulo, seguida da unidade.

Se o resultado for de apenas um dígito, deve ser precedido de zero.

Uma vez que todos os campos estão completos, fazemos uma soma na diagonal.

Ou seja, a soma da primeira diagonal será 0, a segunda será 9, a terceira será 4 e a última será 3.

Desta forma, o resultado final será 943.

Achou mais fácil?

3. Método de matriz (array, em inglês)

Neste método, assim como no anterior, precisamos desenhar uma tabela.

Vamos seguir com o exemplo 23 x 41.

O primeiro passo é decompor os números da operação na tabela, que terá duas colunas e duas linhas.

Em uma coluna, colocamos o 20, e na outra o 3. Nas linhas, inserimos em sentido horário os números 40 e 1.

Multiplicamos então o número de cada coluna com o da linha correspondente.

Os zeros, no entanto, são ignorados.

Sendo assim, em vez de multiplicar 20 por 40, por exemplo, fazemos o cálculo 2 x 4, obtendo 8 como resultado.

O mesmo acontece com 3 x 40. Eliminamos o 0 e multiplicamos 3 x 4, que dá 12. E assim por diante.

Na sequência, acrescentamos ao resultado os zeros que havíamos deixado de lado.

Então, no primeiro cálculo, cujo resultado foi 8, adicionamos os dois zeros eliminados inicialmente, chegando a 800.

No caso de 3 x 4, que dá 12, acrescentamos um zero ao resultado, que vai virar 120.

E assim sucessivamente.

Por fim, somamos o resultado de cada um dos campos da tabela, chegando a 943.

Diversidade

O fato é que, independentemente do método, chega-se ao mesmo resultado.

Mas por que esses métodos não costumam ser ensinados na América Latina?

"A história mostra que, com o passar dos anos, esses métodos foram deixados de lado porque se deu muito mais importância ao cálculo mental na América Latina", disse à BBC Andrea Vázquez, professora de matemática que treina estudantes para participar de concursos nacionais na Argentina.

Mas David Wees, professor de matemática canadense e assessor da New Visions for Public Schools, organização que dá suporte educacional às escolas públicas de Nova York, apresenta outra versão.

"Recentemente, eu li que adotamos esse método é para economizar tinta e papel. E não devido à facilidade do uso. Mas, sim, para preservar esses recursos, já que, quando foram criados, a tinta e o papel eram escassos", conta.

Ele acredita, no entanto, que os métodos alternativos podem ser muito úteis.

"Acredito que não é uma boa prática levar os estudantes diretamente à multiplicação, obrigando-os a decorar tabuadas, sem explicar a eles de onde vêm, porque, caso se esqueçam de uma delas, como poderão calcular a seguinte?"

"O método de multiplicação japonês (ou maia) é bastante necessário porque com ele é possível reconhecer a estrutura geral da multiplicação, e isso pode ser um bom começo", afirma Wees à BBC.

Há ainda outros métodos de multiplicação bem diferentes do tradicional, como o russo ou o egípcio. Mas não exigem a "habilidade extra" de desenhar.

E, segundo especialistas, o atributo visual pode ajudar muita gente a ter uma compreensão melhor do processo de multiplicação.

"Obviamente, tudo ajuda. A matemática no mundo de hoje é aberta dentro e fora das salas de aula", afirma Vázquez.